Visualizing Functions of a Complex Variable

What does it mean to graph a function of a complex variable, w = f(z)?

Let us first consider a real function of a real variable, y = sin(x), for example. The set of points (x,y) which satisfy this can be graphed, for some finite domain, as a 2D picture:

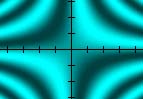
A real function of two variable, z = sin(x*y), for example, can be graphed, over some finite domain, as the height of a 3D surface, a density plot, or a set of contour lines:

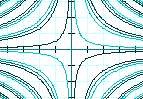The surface on the left is a 3D model of the (x,y,z) points satisfying the equation. The density plot in the middle represents the value of the function at (x,y) as a color. The contour plot on the right shows curves in the (x,y) plane where the function is constant.

A function of a complex variable, w = f(z), can be thought in terms of its real components:

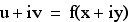
We will demonstrate a number of ways to visualize the set of points (x, y, u, v) satisfying this equation.

Explicitly dropping one of the coordinates allows us to render a 3D surface. We can also encode the remaining coordinate by coloring the surface.
- (x, y, u) can be seen by graphing Re(f(x+iy))
- (x, y, v) can be seen by graphing Im(f(x+iy))
- (x, u, v) can be seen by graphing the real part of the inverse of f.
- (y, u, v) can be seen by graphing the imaginary part of the inverse of f.
- We can also graph the magnitude or phase of f(x+iy).
The points (x, y, u, v) represent a surface in four dimensions. This surface can be drawn using perspective projection in much the same way 3D surfaces are rendered on screen.
We can encode the magnitude and phase of f(x+iy) onto a 2D color map using the hue and intensity to represent the complex value of the function.
We can represent the complex value of the function as a vector, drawing f(x+iy) as a 2D vector plot.
We can consider the complex function as mapping from regions in (x,y) to regions in (u,v) and show how this mapping morphs lines and pictures.

Not all of these techniques are distinct. Color mapping can be used in conjunction with any technique to either encode more information, or to redundantly encode information to make interpretation easier. The 3D surface representations are just a special case of the 4D perspective projection choosing particular views which are easier to understand.

Using 3D models


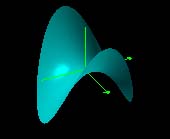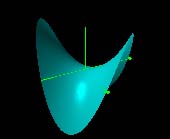Re(z²)	Im(z²)


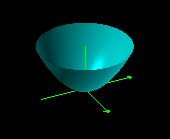\|z²\|	arg(z²)


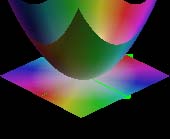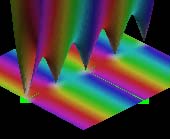\|z²\| color coded by arg(z²)	\|sin πz\| colored by argument

Using 2D color maps


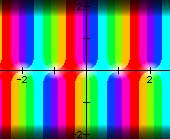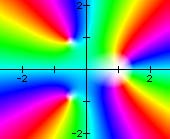sin πz Zeros are white.	(z³ - 1)(z - 1) The color cycles twice at the double root.


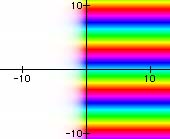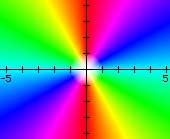e^z	z²

Using 2D vector plots

Using 4D perspective projection

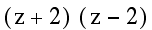
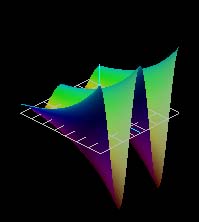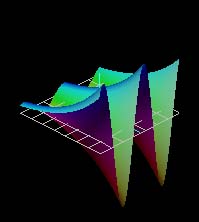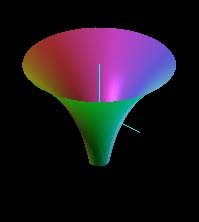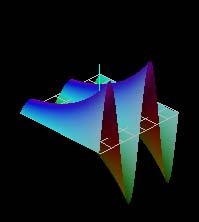
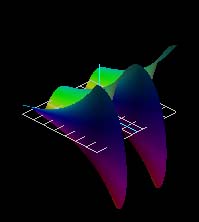
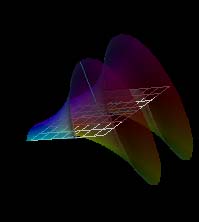
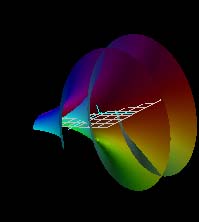
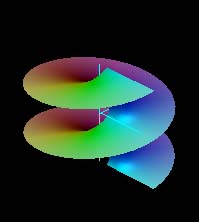
All of the images above are different views of the complex exponential function. In general, one can see the sinusoidal variation along the imaginary or y-axis and exponential variation along the real or x-axis. The white grid is the (x,y) plane at u = v = 0. In some views, it is seen edge-on as a white line segment.

Using conformal maps

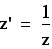
In all the images above, the lines and picture are the left are mapped under the complex inverse function to produce the image on the right.

Notes

If you have installed the free viewer, clicking on an image above will open a corresponding document.

In the color maps, hue indicates phase, saturation and lightness indicate magnitude. Real values are cyan, pure imaginary values are red.